|
Notations
La notation adoptée dans le présent travail est basée sur celle de Peano, et les explications qui suivent sont dans une certaine mesure inspirées
de celles dont il fait précéder son Formulario Mathematico. On lui a emprunté l'emploi des points comme parenthèses, ainsi que plusieurs de ses symboles.
Les variables
L'idée de variable, telle qu'elle figure dans cet ouvrage, est plus générale que celle dont fait explicitement usage la mathématique ordinaire.
Dans la mathématique ordinaire, une variable représente généralement un nombre indéterminé ou une quantité.
En logique mathématique, n'importe quel
symbole dont le sens n'est pas déterminé est appelé une variable, et les diverses déterminations dont ce sens est susceptible sont
appelées les valeurs de la variable. [...] quand dans un manuel de logique on affirme
que « A est A »,
sans autre indication de ce que A peut être, ce que l'on veut dire, c'est que n'importe quel énoncé de la forme
« A est A » est vrai.
[...]
En résumé, les trois faits les plus importants à propos de l'usage de la variable sont :
(1) qu'une variable a une dénotation ambiguë et par conséquent qu'elle est indéterminée ;
(2) qu'une variable préserve une identité reconnaissable en plusieurs occurrences dans le même contexte, de sorte que plusieurs variables peuvent figurer
ensemble dans le même contexte, chacune avec son identité distincte ;
et (3) que soit les parcours de déterminations possibles de deux variables sont identiques, de sorte que la détermination de l'une est aussi la détermination de l'autre,
soit les parcours de deux variables sont différents [...].
L'emploi des différentes lettres
On dénotera les variables au moyen de lettres uniques, et de même pour les constantes ; mais une lettre qui a
été assignée à une constante par une définition ne doit pas être ensuite utilisée pour dénoter une variable. Les petites lettres de l'alphabet ordinaire
seront toutes réservées pour les variables, sauf
p et
s, qui reçoivent, après *40, un sens constant. Les capitales suivantes recevront aussi
des sens constants :
B,
C,
D,
E,
F,
I et
J.
Parmi les petites lettres grecques, nous donnerons un sens constant à
.png) , ,
.png) et (plus loin) à et (plus loin) à
.png) , ,
.png) et et
.png) .
Certaines capitales grecques seront de temps en temps utilisées pour des constantes, mais jamais
pour des variables. Parmi les lettres restantes,
p,
q et
r
seront appelés des lettres propositionnelles, et représenteront des
propositions variables (sauf que, à partir de *40, p ne doit pas être utilisé pour une variable) ;
f,
g, .
Certaines capitales grecques seront de temps en temps utilisées pour des constantes, mais jamais
pour des variables. Parmi les lettres restantes,
p,
q et
r
seront appelés des lettres propositionnelles, et représenteront des
propositions variables (sauf que, à partir de *40, p ne doit pas être utilisé pour une variable) ;
f,
g,
.png) , ,
.png) , ,
.png) et (jusqu'à *33) F seront appelés des lettres fonctionnelles, et seront utilisés pour les fonctions variables.
et (jusqu'à *33) F seront appelés des lettres fonctionnelles, et seront utilisés pour les fonctions variables.
Les petites lettres grecques qui n'ont pas encore été mentionnées seront utilisées pour des variables dont les valeurs sont des classes, et seront simplement
appelées des lettres grecques. Les capitales ordinaires qui n'ont pas encore été mentionnées seront utilisées pour des variables dont les valeurs sont
des relations, et seront simplement appelées des lettres capitales. Les petites lettres ordinaires autres que
p,
q,
r,
s,
f,
g,
seront utilisées pour des variables dont on ne sache pas que les valeurs soient des fonctions, des classes, ou des
relations ; on appellera ces lettres simplement des petites lettres latines.
[...]
Les fonctions fondamentales de propositions
[...] il y en a quatre d'une importance fondamentale, vu que tous les groupements de propositions subordonnées en une proposition complexe
qui figurent dans ce qui suit en sont dérivés par étapes successives.
Il s'agit
,
ou fonction disjonctive,
ou fonction conjonctive,
.
Ces fonctions, tel qu'il y est fait appel dans cet ouvrage, ne sont pas toutes indépendantes ; et si deux d'entre
elles sont prises comme idées primitives non définies, les deux autres peuvent se définir par leur moyen. Le choix des fonctions primitives est jusqu'à un
certain point — quoique pas entièrement — arbitraire. Simplicité des idées primitives et symétrie de traitement semblent être les deux avantages
de donner la préférence aux deux premières fonctions.
avec l'argument p, où p est n'importe quelle proposition, est la contradictoire de p, c'est-à-dire la proposition
affirmant que p n'est pas vrai. Ce qui est dénoté par ~p.
Ainsi ~p est la fonction contradictoire qui a p
pour argument et qui signifie la négation de la proposition p. On s'y référera également comme à la proposition non-p. Ainsi
~p signifie non-p, qui signifie la négation de p.
est une fonction propositionnelle à deux arguments p et q, et est la proposition qui affirme
p ou q
de manière disjonctive, c'est-à-dire qui affirme qu'au moins l'un des deux est vrai.
Ce qui est dénoté par p v q.
Ainsi p v q est la somme logique pour les arguments
p et q. Ce que l'on appelle aussi la somme logique de p et q.
p v q
veut donc dire qu'au moins p ou q est vrai,
sans exclure le cas où les deux le sont.
est une fonction propositionnelle à deux arguments p et q, et est la proposition qui affirme
p et q
de manière conjointe, c'est-à-dire qui affirme que p et q sont tous deux vrais. Ce qui est dénoté par
p • q,
[...].
Ainsi p • q
est le produit logique de p et q.
Par conséquent p • q
veut dire que p et q sont tous deux vrais. Il est facile de voir que cette fonction peut être définie au moyen
des deux fonctions
précédentes. Car quand p et q sont tous deux vrais, il doit être faux que soit p soit q est vrai.
Aussi, dans cet ouvrage,
p • q
est une forme symbolique abrégée de
~ (~p v ~q).
À toute autre idée qui peut être liée à
« p et q sont tous deux
vrais », il n'est pas fait appel ici.
est une fonction propositionnelle à deux arguments p et q, et est la proposition que
soit non-p soit q est vrai, c'est-à-dire que c'est la proposition
~ p v q.
Aussi si p est vrai, ~p est faux, et par conséquent la seule alternative offerte par
la proposition p v q est que q est vrai. En d'autres termes si
p et p v q sont tous deux vrais, alors q est vrai.
On se référera en ce sens à la proposition p v q comme à une proposition énonçant que
p implique q. L'idée contenue dans cette fonction propositionnelle est si importante qu'elle exige une symbolisation
qui représente directement que la proposition connecte p et q sans l'intervention de
~p. Mais « implique »,
tel qu'on l'emploie ici, n'exprime rien d'autre que la connexion entre p et q qui est aussi exprimée par la disjonction
« non-p ou q ».
Le symbole employé pour
« p implique q »,
c'est-à-dire pour
« ~ p v q »,
est « p ⊃ q ».
Ce symbole peut aussi se lire
« si p, alors q ». [...]
Ces quatre fonctions de propositions sont les fonctions propositionnelles constantes
(c'est-à-dire déterminées) qui ont des propositions pour arguments,
et toutes les autres fonctions propositionnelles qui ont des propositions pour arguments, pour autant qu'il y soit fait appel dans le présent travail,
sont formées à partir d'elles en un nombre d'étapes successives. [...]
L'équivalence
Le plus simple exemple de formation d'une fonction complexe de propositions au moyen de ces quatre formes fondamentales nous est fourni par
« l'équivalence ».
Deux propositions p et q sont
dites « équivalentes » quand p implique q
et q implique p. Cette relation entre p et q est dénotée par
« p ≡ q ».
Aussi
« p ≡ q »
représente-t-il
« (p ⊃ q)•(q ⊃ p) ».
Il est facile de voir que deux propositions sont équivalentes quand, et seulement quand, elles sont toutes les deux vraies ou toutes les deux fausses.
[...]
Les valeurs de vérité
La « valeur de vérité »
d'une proposition est le vrai
si elle est vraie, et le faux si elle est fausse.
On observera que les valeurs de vérité de
p v q,
p • q,
p ⊃ q,
~p,
p ≡ q
ne dépendent que de celles de p et de q : la valeur de vérité de
« p v q »
est le vrai si la valeur de vérité de p ou de q est le vrai, et le faux dans les autres cas ;
celle de
« p • q »
est le vrai si celle et de p et de q est le vrai, et le faux dans les autres cas ;
celle de
« p ⊃ q »
est le vrai si soit celle de p est le faux, soit celle de q est le vrai ;
celle de
« ~p » est l'opposé de celle de p ;
et celle de
« p ≡ q »
est le vrai si p et q ont la même valeur de vérité, et le faux dans les autres cas.
Or les seules manières dont les propositions qui figurent dans le présent ouvrage sont dérivées des propositions ci-dessus, sont la combinaison et la répétition.
Aussi est-il facile de voir (quoique cela ne puisse être formellement prouvé pour chaque cas particulier) que si une proposition figure dans une proposition
quelconque f (p) dont nous devons nous occuper, la valeur de vérité de
f (p) dépendra non pas de la
proposition particulière p, mais seulement de sa valeur de vérité,
c'est-à-dire que si
p ≡ q,
nous aurons f (p) ≡ f (q).
Aussi chaque fois que l'on sait que deux propositions sont équivalentes, chacune peut être substituée à l'autre dans toute formule que l'on rencontre.
Le signe d'assertion
Le signe «┣ », appelé « signe d'assertion »,
veut dire que ce qui suit est affirmé.
Il est nécessaire pour distinguer une proposition complète que nous affirmons de toutes les propositions subordonnées qu'elle peut contenir,
mais qui ne sont pas affirmées. Dans l'écriture en langage ordinaire, une phrase encadrée par des points dénote une proposition affirmée, et si elle est fausse,
le livre où elle figure est dans l'erreur. Le signe «┣ » préfixé à une proposition joue le même rôle dans notre symbolisme. Quand on a, par exemple,
«┣ (p ⊃ p) »,
cela doit être considéré comme une assertion complète condamnant ses auteurs à l'erreur, à moins que la proposition
« p ⊃ p »
ne soit vraie (telle quelle). Une proposition formulée dans notre symbolisme sans que le signe
«┣ »
lui soit préfixé n'est pas affirmée, et elle n'est avancée que pour être simplement considérée, ou comme une partie subordonnée d'une proposition affirmée.
Les propositions primitives
Quelques propositions doivent être supposées vraies sans que l'on dispose pour elles de preuves, puisque toute inférence procède à partir de propositions
préalablement affirmées. [...] De telles propositions sont appelées les
« propositions primitives ». Leur choix, comme celui des idées primitives,
est jusqu'à un certain point arbitraire ; quoique, comme dans le cas précédent, plus ces propositions sont simples
et peu nombreuses, plus un système logique a d'importance. On verra que la faible capacité de l'imagination à traiter d'idées très abstraites empêche de
trop mettre l'accent sur leur caractère évident. Elles sont évidentes pour un esprit instruit, mais c'est aussi le cas de plusieurs propositions qui ne
peuvent être tout à fait vraies, parce que réfutées par leurs conséquences contradictoires.
La preuve de la vérité d'un système logique réside dans son
adéquation et sa cohérence. C'est-à-dire :
(1) que le système doit embrasser parmi ses déductions toutes les propositions que nous croyons vraies et capables d'être déduites à partir de seules
prémisses logiques, quoiqu'il faille peut-être y apporter une légère restriction en leur donnant une expression plus rigoureuse ; et
(2) que le système ne doit conduire à aucune contradiction, c'est-à-dire qu'en poursuivant nos inférences nous ne devons jamais être conduits à affirmer à
la fois p et non-p, ou encore qu'il ne peut être légitime qu'apparaissent à la fois
«┣ • p » et «┣ • ~p ».
Les propositions primitives employées dans le calcul des propositions sont les suivantes :
(Les lettres « Pp » veulent dire « proposition primitive ».)
(1)
Tout ce qui est impliqué par une prémisse vraie est vrai Pp.
C'est la règle qui justifie l'inférence.
(2)
┣ : p v p • ⊃ • p
Pp,
c'est-à-dire : si p ou p est vrai, alors p est vrai.
(3)
┣ : q • ⊃ • p v q
Pp,
c'est-à-dire : si q est vrai, alors p ou q est vrai.
(4)
┣ : p v q • ⊃ • q v p
Pp,
c'est-à-dire : si p ou q est vrai, alors q ou p est vrai.
(5)
┣ : p v (q v r)
• ⊃ • q v (p v r)
Pp,
c'est-à-dire que si soit p est vrai, soit
« q ou r »
est vrai, alors soit q est vrai, soit
« p ou r »
est vrai.
(6)
┣ : • q ⊃ r • ⊃ : p v q • ⊃ • p v r
Pp,
c'est-à-dire que si q implique r, alors
« p ou q »
implique
« p ou r ».
(7)
Outre ces propositions primitives, nous avons besoin d'une proposition primitive appelée « l'axiome
d'identification des variables réelles ». [...]
|


![]() Définition de la mathématique pure
Définition de la mathématique pure
![]()
![]() Analyse logique et philosophie
Analyse logique et philosophie
![]()
![]()
![]() Les fonctions propositionnelles
Les fonctions propositionnelles
![]()
![]() Noms propres, adjectifs et verbes
Noms propres, adjectifs et verbes
![]()
![]()
![]()
![]() Le principe du cercle vicieux [paradoxes]
Le principe du cercle vicieux [paradoxes]
![]()
![]() Philosophie de l'atomisme logique
Philosophie de l'atomisme logique
![]()
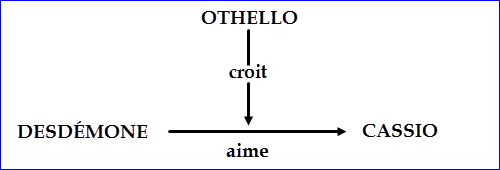
![]() Forme logique d'une croyance (1918)
Forme logique d'une croyance (1918)
![]()
![]() [Le sense-data est privé ; le réel est public]
[Le sense-data est privé ; le réel est public]
![]()